La fórmula de Herón permite calcular el área de un triángulo cuando se conocen las longitudes de sus tres lados. Es particularmente útil cuando no se dispone de la altura del triángulo.
Semiperímetro : Primero, se calcula el semiperímetro del triángulo. El semiperímetro es la mitad del perímetro del triángulo. Si a, b y c son las longitudes de los lados del triángulo, el semiperímetro se calcula así:
Semiperímetro = (a + b + c) /2
Área : Luego, se utiliza el semiperímetro para calcular el área del triángulo con la siguiente fórmula:
- , b y c son las longitudes de los lados del triángulo.
- s es el semiperímetro del triángulo.
- A es el área del triángulo.
Una vez explicada la fórmula que se va a utilizar en la función para calcular el área del triángulo, se procede a explicar otro concepto que se va a utilizar en la fórmula.
Usaremos el operador de exponenciación para encontrar la raíz cuadrada: La raíz cuadrada de x = x elevado a la potencia de 1/2.
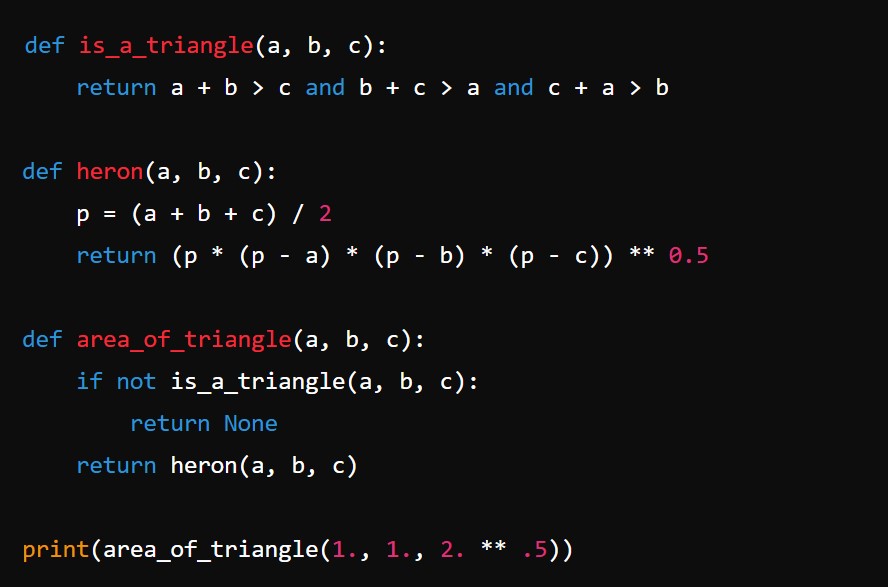
El código de la función contiene tres funciones que trabajan juntas para calcular el área de un triángulo usando la fórmula de Herón.
def is_a_triangle(a, b, c): Esta función verifica si las longitudes dadas pueden formar un triángulo válido.
Entradas de la función: a, b, c (las longitudes de los tres lados del triángulo).
Salida de la función: True si las longitudes pueden formar un triángulo; False en caso contrario.
Lógica de la función: Utiliza la desigualdad triangular que establece que para formar un triángulo, la suma de las longitudes de dos lados siempre debe ser mayor que la longitud del tercer lado. Se verifican las tres condiciones necesarias.
def heron(a, b, c): Esta función calcula el área del triángulo usando la fórmula de Herón.
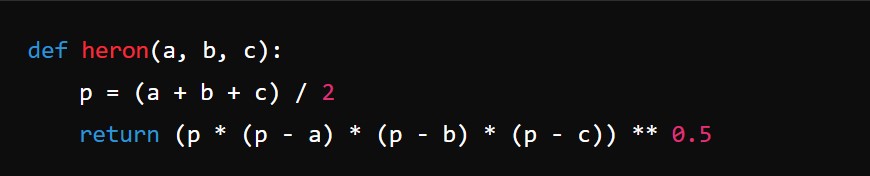
Entradas de la función: a, b, c (las longitudes de los tres lados del triángulo).
Salida de la función: El área del triángulo.
Lógica de la función:
Primero, calcula el semiperímetro p.
Luego, aplica la fórmula de Herón para calcular el área:
def area_of_triangle(a, b, c): Esta función principal utiliza las dos funciones anteriores para calcular el área del triángulo si es válido.
Entradas de la función : a, b, c (las longitudes de los tres lados del triángulo).
Salida de la función: El área del triángulo si es válido; None en caso contrario.
Lógica de la función:
Verifica si las longitudes pueden formar un triángulo utilizando is_a_triangle.
Si es un triángulo válido, calcula el área usando la función heron.
Realizaremos un ejemplo para probar el funcionamiento de la función creada para el cálculo del área de un triángulo:
El área del triángulo con lados 2, 2 y 2 es aproximadamente 1.7321 m2.
Contenido Web de Yolanda Muriel está sujeto bajo Licencia Creative Commons Atribución-NoComercial-SinDerivadas 3.0 Unported.
yolandamuriel.com 