Se va realizar el ejemplo de una función para verificar si tres lados de longitudes dadas pueden formar un triángulo.
Un triángulo con lados iguales:
La suma de dos lados cualesquiera tiene que ser mayor que el tercer lado. La función tendrá tres parámetros: uno para cada lado. La función devolverá True si los lados pueden formar un triángulo, y False en caso contrario. En este caso, is_a_triangle será el nombre para la función.
El código de la función será:
Este código se puede simplificar:
Hemos negado la condición (invertido los operadores relacionales y reemplazado ors con ands, obteniendo una expresión universal para probar triángulos).
Instalemos la función en un programa más grande. Pedirá al usuario tres valores y hará uso de la función.
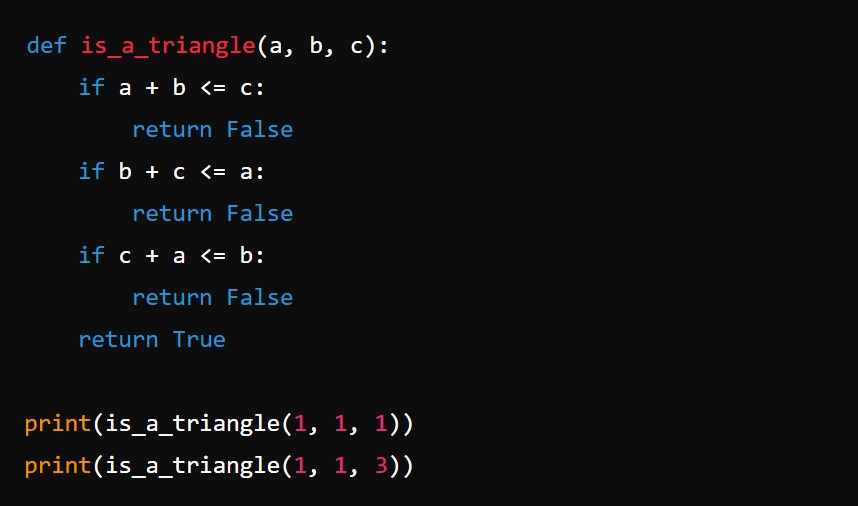
La función is_a_triangle(a, b, c) toma tres argumentos: a, b, y c, que representan las longitudes de los tres lados de un posible triángulo. La función utiliza la desigualdad triangular para determinar si las longitudes dadas pueden formar un triángulo.
Desigualdad Triangular
La desigualdad triangular establece que, para que tres lados formen un triángulo válido, la suma de las longitudes de cualesquiera dos lados debe ser mayor que la longitud del tercer lado. Específicamente:
a+b>c
b+c>a
c+a>b
Cuerpo de la Función
Primera Verificación:
Aquí se verifica si la suma de a y b es menor o igual a c. Si es así, los lados no pueden formar un triángulo, y la función devuelve False.
Segunda Verificación:
Similar a la primera verificación, aquí se verifica si la suma de b y c es menor o igual a a. Si es así, los lados no pueden formar un triángulo, y la función devuelve False.
Tercera Verificación:
Esta verificación comprueba si la suma de c y a es menor o igual a b. Si es así, los lados no pueden formar un triángulo, y la función devuelve False.
Devolver True:
Si ninguna de las condiciones anteriores se cumple, significa que todas las sumas de dos lados son mayores que el tercer lado, por lo que las longitudes pueden formar un triángulo. La función devuelve True.
Ejemplo 1:
Para los lados de longitud 1,1,1:
- 1+1>1(Verdadero)
- 1+1>1 (Verdadero)
- 1+1>1 (Verdadero)
Como todas las condiciones se cumplen, la función devuelve True, indicando que los lados pueden formar un triángulo.
Ejemplo 2:
Para los lados de longitud 1, 1, 3:
1+1>3 (Falso)
1+3>1 (Verdadero)
3+1>1 (Verdadero)
La primera condición es falsa, por lo que la función devuelve False, indicando que los lados no pueden formar un triángulo.
La función is_a_triangle utiliza la desigualdad triangular para verificar si tres longitudes de lados pueden formar un triángulo, devolviendo True si es posible y False en caso contrario. Los ejemplos proporcionados muestran cómo se aplican estas verificaciones a diferentes conjuntos de longitudes de lados.
Contenido Web de Yolanda Muriel está sujeto bajo Licencia Creative Commons Atribución-NoComercial-SinDerivadas 3.0 Unported.
yolandamuriel.com 