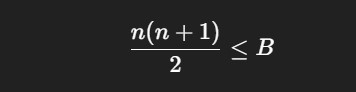REVIT ARCHITECTURE (983) – PYTHON – Bucles (67) – Bucle While

En este artículo se va a aprender a:

• Usar un bucle while.
• Traducir reglas explicadas en lenguaje natural a instrucciones de programación.
• Representar una situación real en código.

Se a a realizar por medio de un ejemplo, que es el siguiente:

Imagina que una niña y su madre tienen un paquete de pegatinas y quieren pegarlas en un álbum. El álbum está organizado de manera que:

• La primera página necesita 1 pegatina,
• La segunda página necesita 2 pegatinas,
• La tercera página necesita 3 pegatinas,
  y así sucesivamente, cada página requiere una pegatina más que la anterior.

Ellas siguen llenando páginas hasta que ya no tienen suficientes pegatinas para completar la siguiente página.

La tarea:
Escribir un programa que reciba como entrada el número total de pegatinas y muestre cuántas páginas del álbum pueden llenarse completamente.

Ejemplo de funcionamiento:

• Entrada: 6 → Salida: Se llenaron 3 páginas completas.
• Entrada: 12 → Salida: Se llenaron 4 páginas completas.
• Entrada: 2 → Salida: Se llenó 1 página completa.

Código en Python:

Explicación línea por línea del código:

1. stickers = int(input("Introduce el número de pegatinas: "))
   • input() pide al usuario que escriba un número en pantalla.
   • int() convierte ese texto introducido en un número entero.
   • Guardamos ese valor en la variable stickers.
2. page = 1
   • La primera página necesita 1 pegatina, así que empezamos con page = 1.
3. filled_pages = 0
   • Esta variable contará cuántas páginas hemos llenado por completo.
   • Comienza en 0 porque aún no hemos llenado ninguna.
4. while stickers >= page:
   • Este bucle se repite mientras tengamos pegatinas suficientes para llenar la página actual.
   • Si no tenemos suficientes pegatinas, el bucle se detiene.
5. stickers -= page
   • Restamos de stickers las pegatinas que usamos para la página actual.
   • Es lo mismo que stickers = stickers - page.
6. filled_pages += 1
   • Aumentamos el contador de páginas llenas en 1.
7. page += 1
   • La siguiente página necesitará una pegatina más que la anterior.
8. print("Se llenaron", filled_pages, "páginas completas.")
   • Mostramos en pantalla el número de páginas llenadas completamente.

Ejemplo de ejecución:

Explicación rápida del ejemplo:

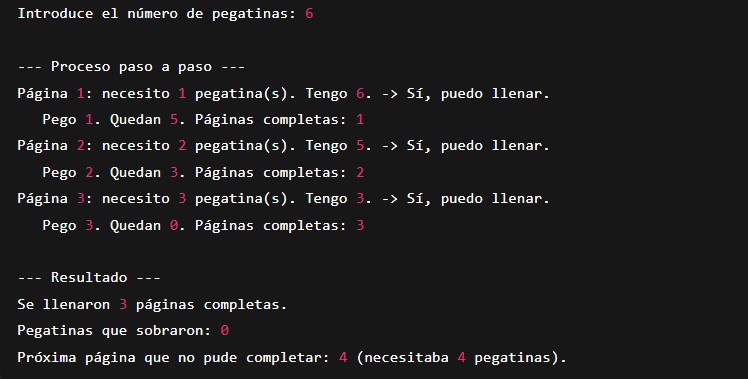
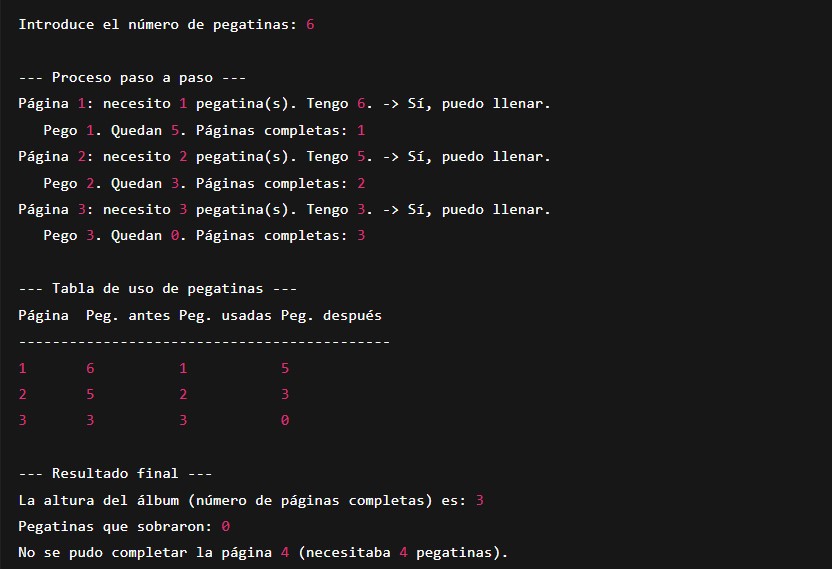
Página 1: usa 1 pegatina → quedan 5.

Página 2: usa 2 pegatinas → quedan 3.

Página 3: usa 3 pegatinas → quedan 0.

No hay suficientes pegatinas para la página 4 → fin.

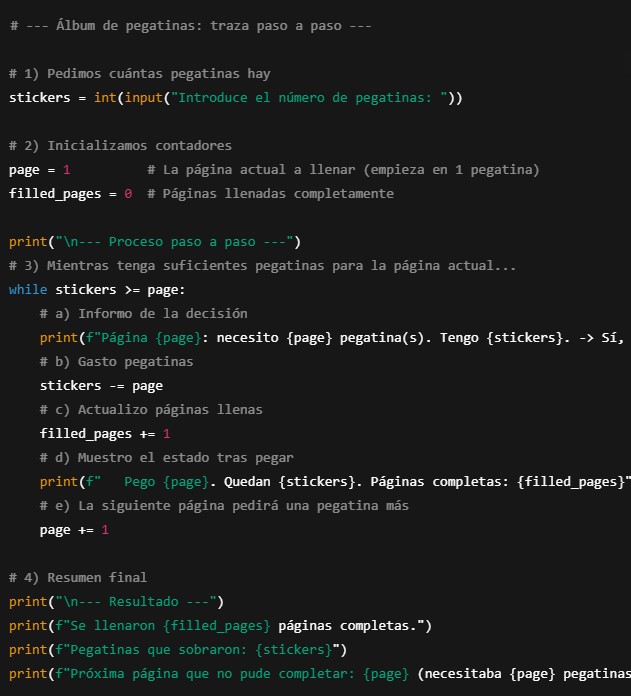
Ahora se va a mostrar un programa que muestra cada iteración del while: qué página intentan llenar, cuántas pegatinas necesitas, cuántas te quedan y el resultado final.

Ejemplo de ejecución (entrada 6)

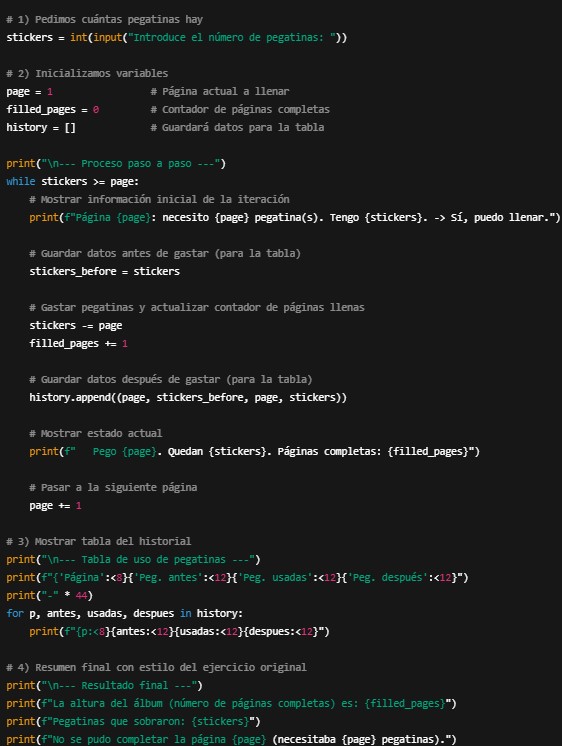
o Más completo,  que muestra el proceso paso a paso.

• Al final presenta una tabla con el historial de páginas, pegatinas usadas y pegatinas restantes.
• Y el texto final se adapta al estilo del ejercicio original.

Ejemplo de ejecución (entrada: 6)

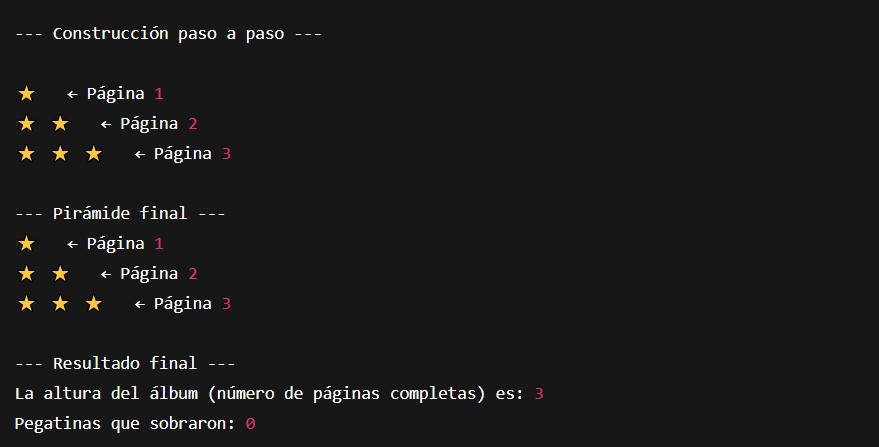
Bonus: Pirámide visual con número de página y modo “animación”

• Cada fila muestra las pegatinas y el número de página.
• Pausa breve entre cada capa para simular cómo se va construyendo.
• Ideal para hacerlo más divertido en clase o en un tutorial.

Ejemplo de salida con entrada 6 (animado)

Este bonus ayuda a:

• Visual y dinámico: ayuda a entender cómo se forman las capas.

• Refuerza el concepto de bucle: se ve claramente cómo en cada iteración se gasta un número creciente de pegatinas.

• Motiva: los estudiantes ven que el código “cobra vida”.

FAQ para Programadores Avanzados

1. ¿Por qué usar while en lugar de for?
   En este problema no sabemos cuántas iteraciones habrá antes de empezar; el número de capas depende del número de pegatinas.
   while es la opción natural porque su condición (stickers >= page) depende de una variable que cambia durante la ejecución.
   Un for sería posible si usáramos un rango arbitrario grande y cortáramos con un break, pero sería menos semántico.
2. ¿Cuál es la complejidad temporal de este algoritmo?
   Es O(n) donde n es el número de capas completas construidas.
   El valor de n es proporcional a la raíz cuadrada del número de pegatinas (porque la suma 1+2+…+n ≈ n²/2).
   Por tanto, en términos de pegatinas B, el tiempo es O(√B), que es muy eficiente incluso para valores grandes.
3. ¿Podría resolverse sin bucles?
   Sí. Si usamos la fórmula de la suma de los n primeros números naturales:

Podemos resolver esta inecuación para n y obtener directamente la altura máxima usando la fórmula cuadrática:

Esto da la altura máxima en O(1) tiempo, pero sacrifica la claridad para estudiantes principiantes.

4. ¿Qué pasa si las reglas cambian y cada página necesita un número diferente de pegatinas?
El código se generaliza fácilmente si reemplazamos page por un cálculo dinámico del coste de la página actual.
Por ejemplo, si el coste crece en progresión geométrica, solo habría que ajustar la lógica dentro del while.

5. ¿Cómo adaptar el código para entrada masiva o streaming de datos?
Si recibimos el número de pegatinas en tiempo real (por ejemplo, un flujo de producción de bloques o pegatinas), podemos mantener un estado interno (stickers, page, filled_pages) y actualizarlo cada vez que llegan nuevos recursos, sin reiniciar el programa.

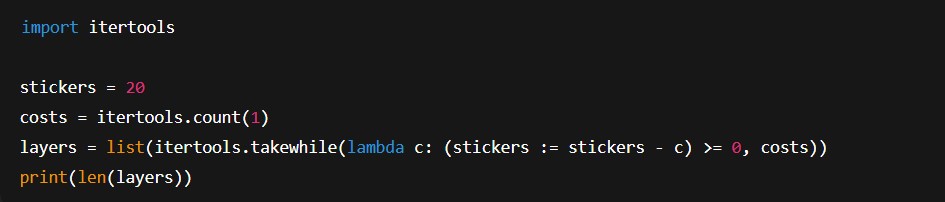
6. ¿Cómo lo harías en un lenguaje funcional?
En Haskell o Scala, por ejemplo, podríamos generar una secuencia infinita de números naturales y usar scanl o takeWhile para acumular hasta agotar las pegatinas.
Ejemplo en Python usando un enfoque funcional:

Retos para Programadores Avanzados

Objetivo: Tomar la idea simple de este problema y ampliarla con variaciones que obliguen a pensar en optimización, algoritmos y estructuras de datos.

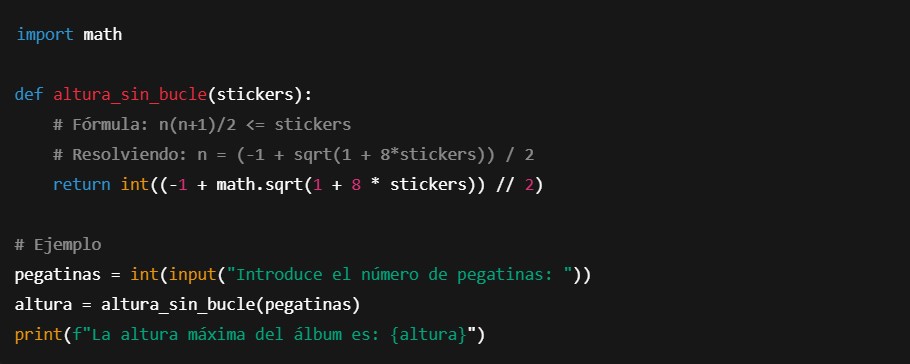
Reto 1 – Fórmula directa sin bucle
Reescribe el programa para calcular la altura del álbum usando únicamente operaciones matemáticas, sin bucles while ni for.
Pista: Usa la fórmula de la suma aritmética y resuelve la ecuación cuadrática.

Reto 2 – Crecimiento no lineal
Modifica las reglas para que:

• La página 1 necesite 1 pegatina,
• La página 2 necesite 3 pegatinas,
• La página 3 necesite 6 pegatinas,
• etc., siguiendo los números triangulares.

Tu programa debe seguir calculando cuántas páginas completas se pueden llenar.

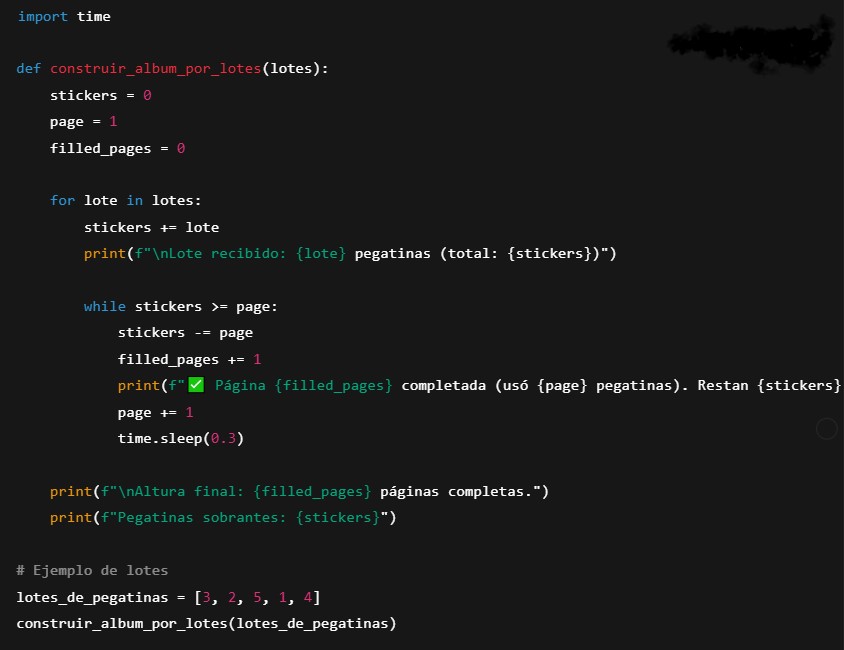
Reto 3 – Pegatinas por lotes
Imagina que las pegatinas llegan en tiempo real en lotes.
Crea un programa que vaya actualizando la pirámide en la pantalla cada vez que llegan nuevas pegatinas, y que muestre si es posible iniciar una nueva página.

Reto 4 – Entrada masiva de datos
Recibe una lista con 10⁶ valores de pegatinas y calcula para cada uno la altura de la pirámide.
Optimiza para que el cálculo sea más rápido que un bucle clásico (hint: precálculo de sumas acumuladas o fórmula matemática).

Reto 6 – Versión orientada a objetos
Implementa una clase AlbumPegatinas con métodos:

• .añadir_pegatinas(cantidad)
• .construir()
• .mostrar_piramide()
  y propiedades como altura, sobrantes, historial.

Reto 7 – Pirámide inversa
Cambia las reglas para que la base empiece con n pegatinas y cada capa tenga una menos que la anterior.
Calcula hasta qué punto puede completarse.

Proponemos que los lectores suban sus soluciones a un repositorio colaborativo (GitHub o Replit) y que compartan capturas de la pirámide generada, fomentando así la interacción. Podéis dejar vuestra información en los comentarios de este artículo o bien en la página de Barcelona Bim en Linkedin ( o bien otros canales).

Reto 1 – Fórmula directa sin bucle. Solución

Usamos la fórmula de la suma aritmética para obtener la altura máxima en O(1).

Ventaja: Calcula la altura instantáneamente sin iteraciones.
Desventaja: No genera la pirámide paso a paso.

Reto 3 – Pegatinas por lotes. Solución

Uso típico: Simulación de datos en streaming o procesos de producción.

 Contenido Web de Yolanda Muriel está sujeto bajo Licencia Creative Commons Atribución-NoComercial-SinDerivadas 3.0 Unported.